[C/C++]다항식 덧셈 프로그램 만들기 - polynomial structure

자료구조 첫번째 게시물이네요.
제가 올리는 코드는 천인국교수님의 C로 쉽게 풀어쓴 자료구조책에 근거하며 책에 있는 코드를 변형하기도하고 분석하는 목적으로 사용됩니다.
다항식 덧셈을 자료구조를 통해 표현해볼겁니다.
총 두가지 방법인데, 첫번째 방법은 식 전체를 한 배열에 저장하는 것이고 두번째 방법은 값이 있는 차수, 계수만 저장하는 것이죠.
천천히 분석해보도록 하겠습니다.
▶다항식 덧셈프로그램 - 모든 차수의 계수값을 저장
#include <stdio.h>
#define MAX(a,b) ((a>b)?(a):(b))
#define MAX_DEGREE 101매크로 상수, 매크로 함수를 이용합니다.
삼중조건문이 매크로 함수에 사용됐는데 a>b가 조건, ? 참일 경우 값 : 거짓일 경우 값 입니다.
typedef struct {
int degree;
float coef[MAX_DEGREE];
}polynomial;구조체와 타입재정의를 이용합니다.
차수는 degree로 표현하고, 계수를 coef로 표현합니다. 한 다항식의 전체 계수를 저장할 것이므로 배열형태인 계수가 필요합니다.
타입재정의를 이용해 지금 구조체를 polynomial로 타입화 합니다.
polynomial poly_add(polynomial A, polynomial B) {
polynomial C;
int Apos = 0, Bpos = 0, Cpos = 0;
int degree_a = A.degree;
int degree_b = B.degree;
C.degree = MAX(A.degree, B.degree);
while (Apos <= A.degree && Bpos <= B.degree) {
if (degree_a > degree_b) {
C.coef[Cpos++] = A.coef[Apos++];
degree_a--;
}
else if (degree_a == degree_b) {
C.coef[Cpos++] = A.coef[Apos++] + B.coef[Bpos++];
degree_a--;
degree_b--;
}
else {
C.coef[Cpos++] = B.coef[Bpos++];
degree_b--;
}
}
return C;
}다항식 덧셈 함수입니다. 반환 해야될 값이 아까 만들어둔 구조체이므로 polynomial 타입을 사용합니다. 인자로 구조체를 받습니다.
Xpos형태로 다항식의 첫 번째 위치를 잡습니다. 인덱스 변수라고 생각하면 되죠. 차수를 미리 입력받아둡니다.
두 다항식의 합에서 결과값의 차수는 큰 쪽을 따라가죠. 아까 매크로 함수 MAX(a,b)를 사용해 결과값의 차수에 넣습니다. 반복문을 이용해 합연산을 합니다. 반복은 다항식 차수까지 진행되며 A의 차수가 클경우, A의 값을 주고, B의 차수가 클 경우 B의 값을 줍니다. 이 때 값은 계수값이죠.
코드를 보면 degree_x--로 되어있습니다. 이건 그냥 최대 차수를 생각하시면 됩니다. 만약 degree가 7이 었다면 x^7에서 x^6의 위치로 이동한 게 됩니다.
차수가 같아질 경우가 나올수 밖에 없는데 이때는 계수의 합을 저장합니다. 합이 모두 다 끝나면 새로 만들어진 구조체 변수를 반환합니다.
void print_poly(polynomial p) {
for (int i = p.degree; i > 0; i--) {
printf("%3.1lfx^%d + ", p.coef[p.degree - i], i);
}
printf("%3.1lf\n", p.coef[p.degree]);
}설명할 게 없는 print 함수입니다. 이 함수를 보면 의아한 점이 있죠. 계수가 합으로 인해 0이 될 경우가 빠져있습니다.
한 줄만 추가해주면 됩니다.
void print_poly(polynomial p) {
for (int i = p.degree; i > 0; i--) {
if (!p.coef[p.degree - i]) continue;
printf("%3.1lfx^%d + ", p.coef[p.degree - i], i);
}
printf("%3.1lf\n", p.coef[p.degree]);
}continue를 이용하면 됩니다.
int main() {
polynomial a = { 5,{3, 6,0,-5,0,1,0} };
polynomial b = { 4,{7,0,5,0,1} };
polynomial c;
print_poly(a);
print_poly(b);
c = poly_add(a, b);
print_poly(c);
gets();
return 0;
}메인함수입니다. gets는 실행파일을 실행했을 때 입력값이 없어 바로 꺼지는 경우를 막기 위해 넣어뒀습니다.
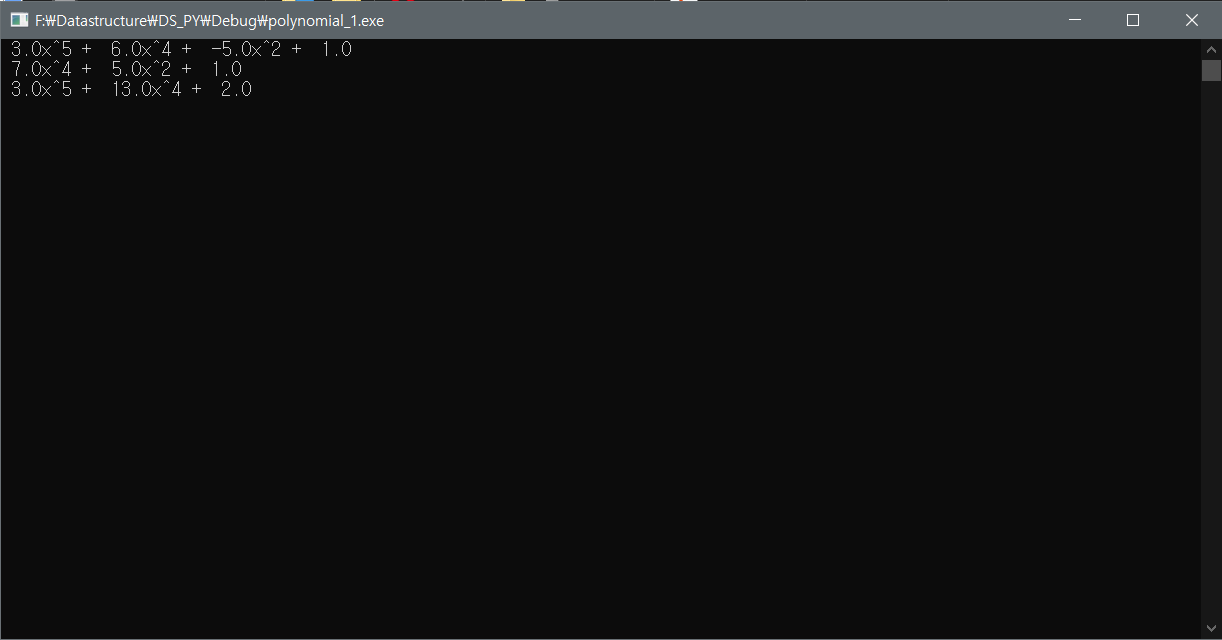
잘 작동하는 것을 볼 수 있습니다.
하지만 이런 계수 전체를 배열로 저장하는 방식은 공간낭비가 심합니다. 두번째 방법에서는 희소행렬을 다룰 때 처럼 다항식 덧셈을 바꿔보겠습니다.
▶다항식 덧셈프로그램 - 모든 차수의 계수값을 저장
#include <stdio.h>
#include <stdlib.h>
//Buffer overrun while writing to 'terms' : the writable size is '808' bytes, but 'avail' bytes might be written.
#define MAX_TERMS 101stdlib 헤더파일을 안쓰려고 했는데 주석처리 해놓은 것 처럼 경고 메시지가 나와서 추가해줬습니다. 이번에는 TERMS를 이용합니다. 항의 배열이라고 생각하면 됩니다.
typedef struct {
float coef;
int exp;
}polynomial;
polynomial terms[MAX_TERMS] = { {8,3},{7,1},{1,0},{10,3},{3,2},{1,0} };
int avail = 6;계수가 단일변수입니다. 항을 표현하기 때문이죠. terms 가 항의 배열로, 각 항이 {coef,exp}형태입니다.
avail은 추가될 항의 위치를 가리키는 인덱스 변수입니다.
typedef를 이용해 구조체배열을 만들었기 때문에 strlen을 사용하지 못해 값을 지정해줬습니다.
char compare(int a, int b) {
if (a > b) return '>';
else if (a == b) return '=';
else return '<';
}
void print_poly(int s, int e) {
for (int i = s; i < e; i++) {
printf("%3.1lfx^%d + ", terms[i].coef, terms[i].exp);
}
printf("%3.1lfx^%d\n", terms[e].coef, terms[e].exp);
}분석할 게 없는 두 함수입니다. compare함수는 뒤에 사용될 switch를 위한 함수입니다. 항의 배열로 다항식을 넣어뒀기 때문에 다항식의 시작항, 종료항을 가리키는 인덱스가 필요합니다. 여기서는 s(start), e(end)로 표현했습니다.
void attach(float coef, int exp) {
if (avail > MAX_TERMS) {
fprintf(stderr, "항 개수가 많음");
exit(1);
}
terms[avail].coef = coef;
terms[avail].exp = exp;
avail++;
}attach함수가 하는 일은 항을 추가하는 것입니다. 항이 구조체배열 크기를 초과할 경우 오류 메시지를 뱉게 방어적코딩을 했습니다.
avail이 가리키는 위치에 항을 추가한 뒤에는 avail++를 해줍니다. C언어는 절차지향이기 때문에 terms[avail++].exp = exp; 로 해도 됩니다.
void poly_add(int As, int Ae, int Bs, int Be, int* Cs, int* Ce) {
float tmp_coef;
*Cs = avail;
while (As <= Ae && Bs <= Be) {
switch (compare(terms[As].exp,terms[Bs].exp))
{
case '>':
attach(terms[As].coef, terms[As].exp);
As++;
break;
case '=':
tmp_coef = terms[As].coef + terms[Bs].coef;
if (tmp_coef) attach(tmp_coef, terms[As].exp);
As++;
Bs++;
break;
case '<':
attach(terms[Bs].coef, terms[Bs].exp);
Bs++;
break;
default:
break;
}
}
for (; As <= Ae; As++) attach(terms[As].coef, terms[As].exp);
for (; Bs <= Be; Bs++) attach(terms[Bs].coef, terms[Bs].exp);
*Ce = avail - 1;
}덧셈함수입니다. Cs와 Ce가 포인터형태인 이유는 값을 돌려줘야 하기 때문입니다. int* Cs가 아닌 int Cs로 한다면 poly_add함수의 반환값이 없으므로 아무것도 변하지 않겠죠.
결과값을 넣을 다항식의 시작이 *Cs, 끝이 *Ce입니다. switch와 compare함수를 이용해서 차수 비교를 합니다.
과정은 비슷합니다. 차수가 같을 경우에 tmp_coef를 이용해서 처음부터 계수합이 0일 때를 제외합니다.
while로 피연산식 두 개가 다 합해지고나서, 연산에 사용되지않은 값들을 attach로 avail에 밀어줍니다.
마지막에 연산이 다 끝나고 avail-1값을 *Ce에 넣어줘 마지막 유효항의 위치를 가리켜줍니다.
int main() {
int As = 0, Ae = 2, Bs = 3, Be = 5, Cs, Ce;
poly_add(As, Ae, Bs, Be, &Cs, &Ce);
print_poly(As, Ae);
print_poly(Bs, Be);
print_poly(Cs, Ce);
gets();
return 0;
}
메인 함수입니다.
이번 경우에는 피연산 다항식 두개가 같은 항의 크기를 가지고 있어서 poly_add의 나머지항을 밀어넣는 코드가 의미없었습니다. 만약 As = 0, Ae = 3으로 A식과 B식의 항 개수차이가 났다면 연산이 다 끝나고 Ae에 위치하는 항이 Ce에 저장됐겠죠.
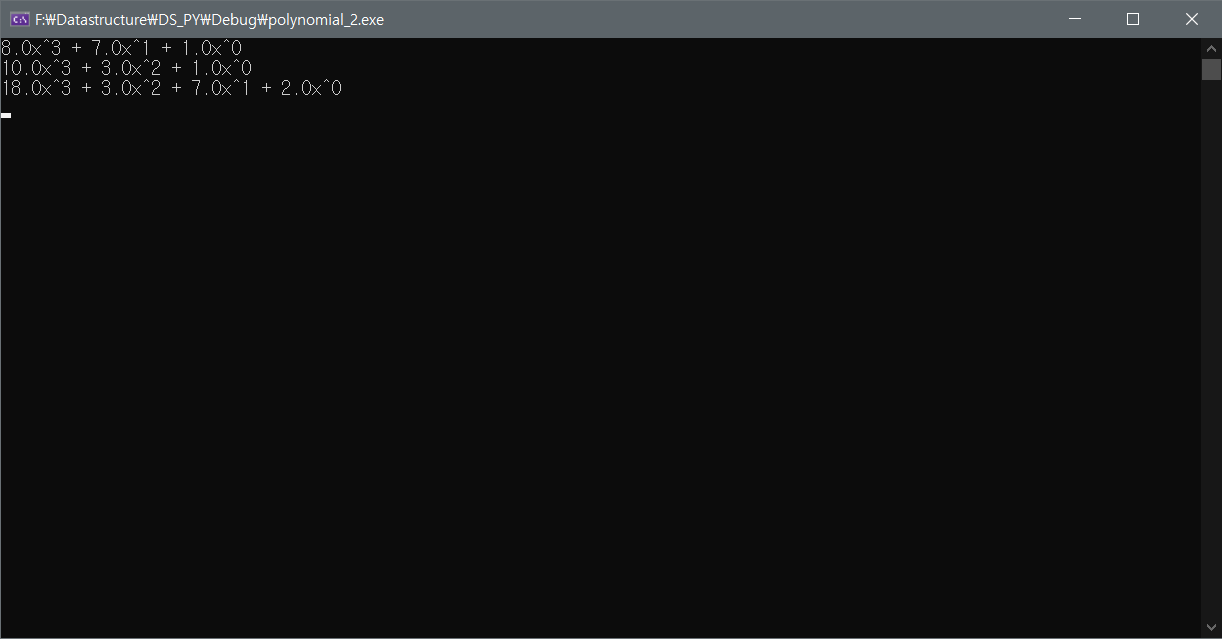
잘 작동합니다.
이번 글에서는 덧셈만 다뤄보았는데 뺄셈의 경우에는 고려해야할 게 몇 가지 있습니다.
1.어떤 식에서 무슨 식을 뺄 건지.(X-Y)
2.같은 차수에서 뺄셈의 경우 음수가 생길수 있음
3.나머지항을 밀어넣을 때 앞 식(X)인지 뒷 식(Y)인지
이 세가지를 추가하면 형태는 거의 비슷하게 나옵니다.
다음 글은 전치행렬, 희소행렬이 될 것 같네요. 희소행렬은 위에서 언급했지만 항을 따로따로 다루는 형태입니다.
"댓글, 공감 버튼 한 번씩 누르고 가주시면 큰 힘이 됩니다"





